반응형
🧱 1. 수 체계의 전체 틀 (Number System Overview)
복소수 (Complex Numbers, ℂ)
├─ 실수 (Real Numbers, ℝ)
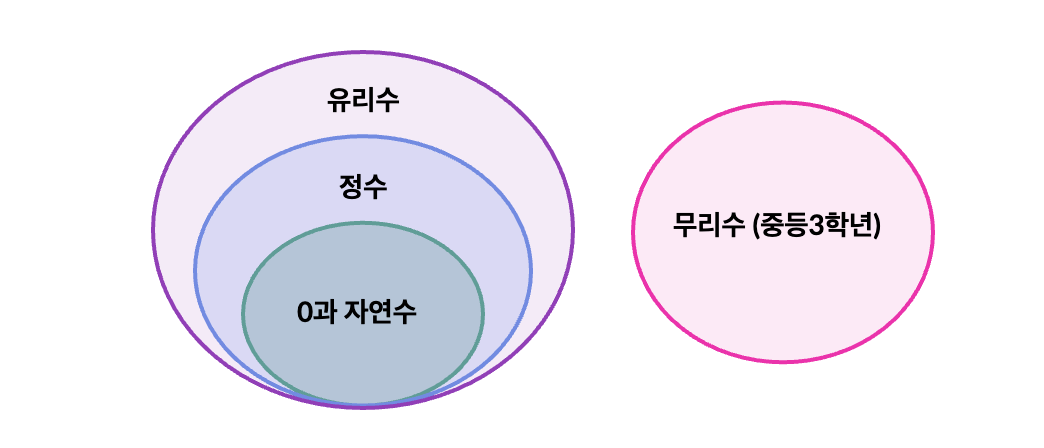
│ ├─ 유리수 (Rational Numbers, ℚ)
│ │ ├─ 정수 (Integers, ℤ)
│ │ │ ├─ 자연수 (Natural Numbers, ℕ)
│ │ │ └─ 음의 정수 (Negative Integers)
│ │ └─ 분수, 순환소수, 유한소수 (Decimals 포함)
│ └─ 무리수 (Irrational Numbers)
│ └─ √2, π,e 등
└─ 허수 (Imaginary Numbers)
└─ i = √–1
📗 2. 각 수 개념별 설명 및 예시
| 분류 | 영문 | 정의 | 예시 | 특징 |
| 자연수 | Natural Numbers (ℕ) | 1부터 시작하는 셈 수 | 1, 2, 3, ... | 0 포함 여부는 상황에 따라 다름 |
| 정수 | Integers (ℤ) | 음수, 0, 양수 모두 포함 | –3, 0, 4 | 소수점 없음 |
| 유리수 | Rational Numbers (ℚ) | 정수 a, b (b≠0)에 대해 a/b로 표현 가능 | ½, –3, 0.75, 2 | 유한소수, 순환소수 포함 |
| 무리수 | Irrational Numbers | a/b 형태로 표현 불가, 무한 비순환 소수 | √2, π, e | 소수점이 끝없이 비반복 |
| 실수 | Real Numbers (ℝ) | 유리수 + 무리수 | –3, 0, √2, π | 수직선 위의 모든 점 |
| 복소수 | Complex Numbers (ℂ) | 실수부 + 허수부 형태 | 2 + 3i, –1 + 0i | 전기공학·파동 분석 등 사용 |
| 허수 | Imaginary Numbers | i² = –1을 기본 단위로 함 | i, 4i, –2i | 복소수의 구성 요소 |
| 소수 | Prime Numbers | 1과 자기 자신만으로 나누어 떨어지는 자연수 | 2, 3, 5, 7, 11 | 1은 소수가 아님 |
| 합성수 | Composite Numbers | 1과 자기 자신 외에 다른 약수가 있음 | 4, 6, 8, 9 | 소수의 반대 개념 |
| 소수 (소숫점) | Decimal Numbers | 정수와 소수점으로 이루어진 수 | 0.5, –3.75 | 유리수 또는 무리수일 수 있음 |
| 유한소수 | Terminating Decimal | 소수점이 끝나는 수 | 0.25 = ¼ | 유리수 |
| 순환소수 | Repeating Decimal | 소수점 뒤에 일정 숫자가 반복됨 | 0.333... = ⅓ | 유리수 |
| 무한소수 | Infinite Decimal | 소수점이 끝없이 이어짐 | π = 3.14159... | 무리수인 경우 비순환 |
| 분수 | Fraction | a/b 형태의 수 | ⅔, –4/5 | 유리수의 대표 형태 |
| 정수배 | Integer Multiple | 어떤 수 × 정수로 표현 | 3n, 2k | 배수 개념 포함 |
| 약수/배수 | Divisor / Multiple | 어떤 수를 나누거나 곱해 만든 수 | 2는 4의 약수 | 소인수분해와 연계 |
| 지수수 | Exponential Number | a^n 꼴의 수 | 2³ = 8 | 거듭제곱, 로그 등과 관련 |
| 로그수 | Logarithmic Number | 지수의 역함수로 정의된 수 | log₂8 = 3 | 대수적 계산 필수 요소 |
📘 3. 소수 vs 소수 (prime vs decimal)
| 용어 | 의미 | 예시 | 혼동 주의 |
| 소수 (Prime Number) | 약수가 1과 자기 자신뿐인 자연수 | 2, 3, 5, 7, 11 | 수론, 암호학 |
| 소수 (Decimal Number) | 소수점이 있는 수 | 0.1, 1.75, π | 실수 내 표현 방식 |
반응형



